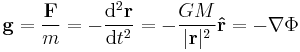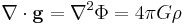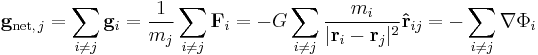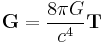Gravitational field

The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses. Following Newton, Laplace attempted to model gravity as some kind of radiation field or fluid, and since the 19th century explanations for gravity have usually been sought in terms of a field model, rather than a point attraction.

In a field model, rather than two particles attracting each other, the particles distort spacetime via their mass, and this distortion is what is perceived and measured as a "force". In such a model one states that matter moves in certain ways in response to the curvature of spacetime,^[1] and that there is either no gravitational force,^[2] or that gravity is a fictitious force.^[3]

1 Classical mechanics
2 General relativity
3 Generally accepted fundamental hypothesis
4 See also
5 Notes

Classical mechanics

In classical mechanics as in physics, the field is not real, but merely a model describing the effects of gravity. The field can be determined using Newton's law of universal gravitation. Determined in this way, the gravitational field around a single particle is a vector field consisting at every point of a vector pointing directly towards the particle. The magnitude of the field at every point is calculated applying the universal law, and represents the force per unit mass on any object at that point in space. Because the force field is conservative, there is a scalar potential energy per unit mass at each point in space associated with the force fields, this is called gravitational potential ^[4]. The field equation is as follows: ^[5]

$\bold{g} = \frac{\bold{F}}{m} = - \frac{{\rm d}^2\bold{r}}{{\rm d}t^2} = - \frac{GM}{|\bold{r}|^2}\bold{\hat{r}} =-\nabla\Phi \,\!$

where:

M = gravitational mass of attracting body,
r = position of a test mass m, and $\scriptstyle \bold{\hat{r}}\,\!$ is a unit vector in the direction of r,
t = time,
∇ is the del operator
Φ = gravitational potential,
G = gravitational constant,
F is the gravitational force.

and contains Newton's law of gravitation, and the relation between gravitational potential and field acceleration. Note that d²r/dt² and F/m are both equal to the gravitational acceleration g (equivalent to the inertial acceleration, so same mathematical form, but also defined as gravitational force per unit mass ^[6]). The negative signs are inserted since the force acts antiparallel to the displacement. The equivalent field equation in terms of mass density ρ of the attracting mass are:

$\nabla\cdot\bold{g} = \nabla^2\Phi = 4\pi G \rho \,\!$

which contains Gauss' law for gravity, and Poisson's equation for gravity. Newton's and Gauss' law are mathematically equivalent, and are related by the divergence theorem. Poisson's equation is obtained by taking the divergence of both sides of the previous equation. These classical equations are differential equations of motion for a test particle in the presence of a gravitational field, i.e. setting up and solving these equations allows the motion of a test mass to be determined and described.

The field around multiple particles is simply the vector sum of the fields around each individual particle. An object in such a field will experience a force that equals the vector sum of the forces it would feel in these individual fields. This is mathematically: ^[7]

$\bold{g}_{{\rm net}, \, j} = \sum_{i\neq j} \bold{g}_i = \frac{1}{m_j} \sum_{i \neq j} \bold{F}_i = - G\sum_{i \neq j}\frac{m_i}{|\bold{r}_i-\bold{r}_j|^2}\bold{\hat{r}}_{ij} =-\sum_{i \neq j}\nabla\Phi_i \,\!$

i.e. the gravitational field on mass m_j is the sum of all gravitational fields due to all other masses m_i, except of course the mass m_j itself. The unit vector 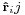$\scriptstyle \bold{\hat{r}}_ij\,\!$ is in the direction of r_i - r_j.

General relativity

In general relativity the gravitational field is determined as the solution of Einstein's field equations: ^[8]

$\bold{G}=\frac{8\pi G}{c^4}\bold{T} \,\!$

These equations are dependent on the distribution of matter and energy in a region of space, unlike Newtonian gravity, which is dependent only on the distribution of matter. The fields themselves in general relativity represent the curvature of spacetime. General relativity states that being in a region of curved space is equivalent to accelerating up the gradient of the field. By Newton's second law, this will cause an object to experience a fictitious force if it is held still with respect to the field. This is why a person will feel himself pulled down by the force of gravity while standing still on the Earth's surface. In general the gravitational fields predicted by general relativity differ in their effects only slightly from those predicted by classical mechanics, but there are a number of easily verifiable differences, one of the most well known being the bending of light in such fields.

Generally accepted fundamental hypothesis

Dr. Jesse L. Greenstein of the California Institute of Technology wrote:

The detection of gravitational waves bears directly on the question of whether there is any such thing as a "gravitational field," which can act as an independent entity. … this fundamental field hypothesis has been generally accepted without observational support. Such credulity among scientists occurs only in relation to the deepest and most fundamental hypotheses for which they lack the facility to think differently in a comparably detailed and consistent way. In the nineteenth century a similar attitude led to a general acceptance of the ether ….^[9]

Most scientists believe that the gravitational field and its gravitational waves are the physical interpretations of Einstein's equations of general relativity.

Notes

^ Geroch, Robert (1981). General relativity from A to B. University of Chicago Press. p. 181. ISBN 0-226-28864-1. http://books.google.com/books?id=UkxPpqHs0RkC&pg=PA181. , Chapter 7, page 181
^ Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer Japan. p. 256. ISBN 0-387-69199-5. http://books.google.com/books?id=IyJhCHAryuUC. , Chapter 10, page 256
^ J. Foster, J. D. Nightingale, J. Foster, J. D. Nightingale; J. Foster, J. D. Nightingale, J. Foster, J. D. Nightingale (2006). A short course in general relativity (3 ed.). Springer Science & Business. p. 55. ISBN 0-387-26078-1. http://books.google.com/books?id=wtoKZODmoVsC. , Chapter 2, page 55
^ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978 0 470 01460 8
^ Encyclopaedia of Physics, R.G. Lerner, G.L. Trigg, 2nd Edition, VHC Publishers, Hans Warlimont, Springer, 2005
^ Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0 7195 3382 1
^ Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, Mc Graw Hill (UK), 1973, ISBN 07-084018-0.
^ Gravitation, J.A. Wheeler, C. Misner, K.S. Thorne, W.H. Freeman & Co, 1973, ISBN 0-7167-0344-0
^ Astronomy and Astrophysics for the 1970s, Report of the United States National Academy of Sciences, Washington, DC, 1972.

Gravitational field

Contents

Classical mechanics

General relativity

Generally accepted fundamental hypothesis

See also

Notes